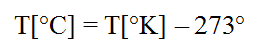Mesurer les températures des étoiles
Équipement recommandé : Lhires III, eShel, Lisa, Alpy, Star Analyser
Durée : 4h
Le philosophe français Auguste Comte (1798-1857) s’est rendu tristement célèbre pour son 19ème cours de philosophie positive exposé en 1835 où il écrivait: « …je n’en persiste pas moins à regarder toute notion sur les véritables températures moyennes des différents astres comme devant nécessairement nous être à jamais interdite ».
Sans doute Auguste Comte n’avait pas eu connaissance des travaux de Joseph Fraunhofer (1787-1826) qui avait dès 1814 étudié dans le détail le spectre solaire et les multiples raies d’absorption qui lui étaient visibles. Nous allons montrer dans cet article qu’avec de modestes moyens, l’astronome amateur d’aujourd’hui peut mesurer les températures d’étoiles en analysant la forme globale du spectre – ce avec une précision moyenne mais correcte compte tenu des moyens employés.
Au début du XXème siècle, le physicien Max Planck (1855-1947) a donné la forme mathématique de la distribution de l’énergie émise par un corps noir. A partir de ces travaux, Albert Einstein (1879-1955) expliqua en 1905 l’effet photoélectrique et en conclua que la lumière était constituée de particules discrètes – les photons. Depuis, la double personnalité de la lumière, à la fois onde et particule, a fait l’objet de nombreuses expériences. Un photon est une particule électriquement neutre et sans masse qui voyage en ligne droite. Son énergie est inversement proportionnelle à sa longueur d’onde l : E = hc/l avec h la constante de Planck (6.62.10-34 J.s) et c la vitesse de la lumière dans le vide (299792 km.s-1).
Cette analyse du photon corpusculaire ouvra la voie à Sir Arthur Schuster (1851-1934) & M. Schwarzschild (1873-1916) sur les théories d’atmosphère des étoiles et permit les premières estimations quantitatives de températures stellaires par les astronomes allemand de Postdam J. Wilsing (1856-1943) & J. Scheiner (1858-1914).
La température est définie par l’agitation des particules. L’air chaud caractérise une agitation des molécules d’air plus forte que pour l’air froid. Pour une étoile, on définit la température effective comme une caractéristique de l’agitation des particules avec comme signe distinctif le rayonnement émis par l’astre.
Le rayonnement qui nous vient des étoiles est produit par la couche externe appelée la photosphère. Elle est en fait très fine par rapport à la taille de l’étoile. Les photons émis du coeur mettent des millions d’années pour parcourir les différentes couches de l’étoile, non pas parce que l’étoile est grande mais parce que les températures internes sont extrèmement élevées et que les photons sont rapidement absorbés et réémis dans d’autres direction.
La lumière parcours ainsi l’intérieur des étoiles par absorption/émission dans tous les sens, d’où un temps très long pour atteindre la photosphère et enfin sortir de l’étoile. Après, la vie du photon est un long fleuve tranquille (et rectiligne) et il a très peu chance de toucher une particule… jusqu’au mirroir de votre télescope!
Loi de Planck
En première approximation, le rayonnement de la photosphère d’une étoile est celui d’un corps noir. Il m’est toujours apparu bizarre de considérer une étoile qui brille de milles feux comme un corps noir. Mais la meilleur analogie est la plaque chauffante de votre cuisinière: à froid, elle est noir et ne réfléchit pas de lumière; à chaud, elle s’illumine.
Les étoiles font de même. Une étoile de température nulle ne brillerait pas et ne réfléchirait aucune lumière. Les théoriciens imaginent les étoiles comme des boîtes noires où rien de rentre et dont le rayonnement n’est lié qu’à sa température d’agitation des particules qui la compose. Mais comment la voit-on? Il suffit d’imaginer un petit trou qui laisse quand même passer le rayonnement vers l’extérieur…
La propriété intéressante du du rayonnement d’un corps noir de température T [°K] est que son intensité à la longuer d’onde l [m] est donnée par la loi de Planck :
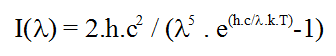
avec k la constante de Boltzmann (1.38.10-23 J.K-1), h la constante de Planck et c la vitesse de la lumière dans le vide.
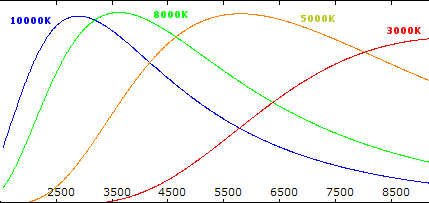
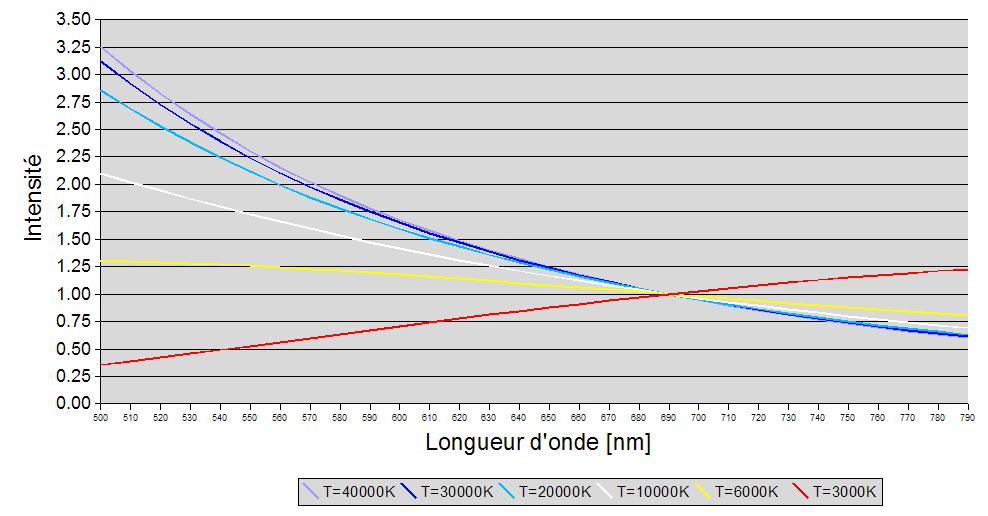
Courbes de Planck pour diverses température T
La loi de Wien
C’est en analysant les spectres émis par des corps noirs à différentes températures que Wilhelm Wien découvrit, en 1893, que la lumière se distribue autour d’une longueur d’onde privilégiée: le pic d’émissivité, inversement proportionnel à la température. La forme du profil du spectre d’u corps noir est très caractéristique, en forme de cloche asymétrique (voir fig.1). Le sommet de la courbe, qui correspond à la longueur d’onde du pic d’émissivité, est donnée par la loi de Wien :
L’unité officielle de la température est le kelvin (K) qui correspond à la température minimum d’un corps, le zéro absolu. A cette température (théorique), les particules constituant ce corps ne présentent plus aucun mouvement. Pour obtenir la température en degrés Celsius, il faut enlever 273° à la température exprimée en Kelvin :
Sur un spectre d’étoile, le profil du spectre est celui d’un corps noir et le pic d’émissivité permet de calculer la température de surface de l’astre. Ainsi, le Soleil qui a son pic d’émissivité vers 500nm, dans le vert, a une température de surface de 5800K.
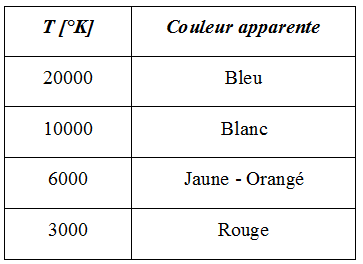
Une étoile plus chaude aura son pic d’émissivité dans le bleu; une étoile plus froide que le Soleil aura son pic dans le rouge. Le tableau suivant donne la couleur apparente d’une étoile en fonction de sa température de surface :
A noter qu’une étoile, quelque soit sa température de surface, émet dans toutes les longueurs d’onde. Sa couleur vue d’une planète environnante serait banche. C’est quand l’étoile est trop éloignée, et assimilée à un point, que sa couleur est dépendante du pic d’émissivité. La couleur peut toutefois être modifiée par des fortes raies d’émission ou d’absorption pour des étoiles particulières.
La loi de Stefan-Boltzmann
Quand la température d’un corps noir augmente, la loi de Wien indique que la longueur d’onde du pic d’émissivité décroît. Mais l’aire définie par le profil spectral, l’intensité totale de la lumière, augmente. En 1879, Josef Stefan découvrit que la lumière émise par chaque mètre carré de la surface d’un objet chauffé est proportionnelle à la puissance quatre de la température en kelvins; cette loi fut démontrée en 1884 par Ludwig Boltzmann (1844-1906). La quantité de lumière émise par chaque mètre carré d’un corps noir est appelée luminosité surfacique (l) et est définie par la loi de Stefan-Boltzmann :
A noter que grâce aux lois de Wien et de Stefan-Boltzmann, on peut déterminer le diamètre des étoiles dont la distance est connue, par mesure de parallaxe par exemple.
Acquisition des spectres avec un Star Analyser
Les spectres qui illustrent cet article ont été pris par Alexandre Santerne avec le Schmidt-Cassegrain Criterion de 200mm de diamètre et 2.1m de focale du Centre d’Etude Spatiale des Rayonnements. La monture est une EQ6 et la caméra CCD une Audine avec un KAF401 simple sans obturateur.
Le spectroscope utilisé est un Star Analyser; il s’agit d’un réseau de 100 traits/mm monté dans un anneau, comme un filtre astronomique au standard 31.75mm. Il se fixe simplement devant la caméra CCD. C’est un moyen simple de débuter en spectroscopie et il est très bien adapté à ce type de mesures de forme globale du spectre de part sa basse résolution.
équipement lors de la prise de vue des spectres
Les spectres obtenus sont assez larges (dérive pendant l’acquisition). Cela est nécessaire dans le cas de l’utilisation d’une caméra couleur (ex: appareil photo numérique) avec des pixels de couleurs différentes juxtaposés, comme dans une matrice de Bayer. Cela évite de concentrer la région bleue du spectre sur un pixel rouge par exemple! Dans le cas d’une caméra CCD monochrome comme ici, ce n’était pas indispensable si ce n’est éviter de saturer le capteur vu la brillance des cibles pointées.
Fig. 3 : spectre brut de Regulus
Fig. 4 : spectre brut d’Antares
Les spectre obtenus montrent déjà des différences entre les spectres de plusieurs étoiles… la magie de la spectroscopie opère déjà!
Extraction du profil spectral
Les spectres obtenus sont inclinés et parfois mal orientés. La première opération à faire est de corriger la géométrie afin d’avoir des spectres horizontaux, des raies bien verticales, le bleu à gauche (convention en astronomie). Nous utilisons pour cela le logiciel IRIS disponible gratuitement et écrit par Christian Buil.
Voici comme exemple les commandes utilisées pour Antares; tous les spectres de la nuit sont ainsi traités :
>load antares
>sub dark 0
>visu 6000 0
>rot 718 194 3
>slant 194 3
La fonction ROT fait une rotation autour d’un point; la fonction SLANT corrige l’inclinaison des raies spectrales.
L’opération suivante est de mettre le fond du ciel à zéro (fonction L_SKY3) puis d’extraire le profil spectral, c’est-à-dire l’intensité du spectre pour chaque colonne de l’image. Une simple addition ou médiane des lignes ne suffit généralement pas; une extraction optimisée (fonction L_OPT) est préférable:
>l_sky 29 72 329 372
>mirrory
>l_opt
>save bin_antares
A noter que la fonction L_OPT retourne une image de 20 pixels de hauteur. C’est uniquement pour faciliter la lecture, chaque ligne étant identique. Une image d’un pixel de haut (ie: un profil) est équivalent.
Calibration des spectres
L’opération suivante consiste à calibrer le profil spectral. Nous utiliserons pour cela le logiciel VisualSpec également disponible gratuitement et écrit par Valérie Desnoux. Pour charger le profil spectral non calibré obtenu avec IRIS, ouvrir d’abord l’image (dans l’exemple précédent: « bin_antares.fit ») puis la convertir en graphe avec l’opération de « binning ».
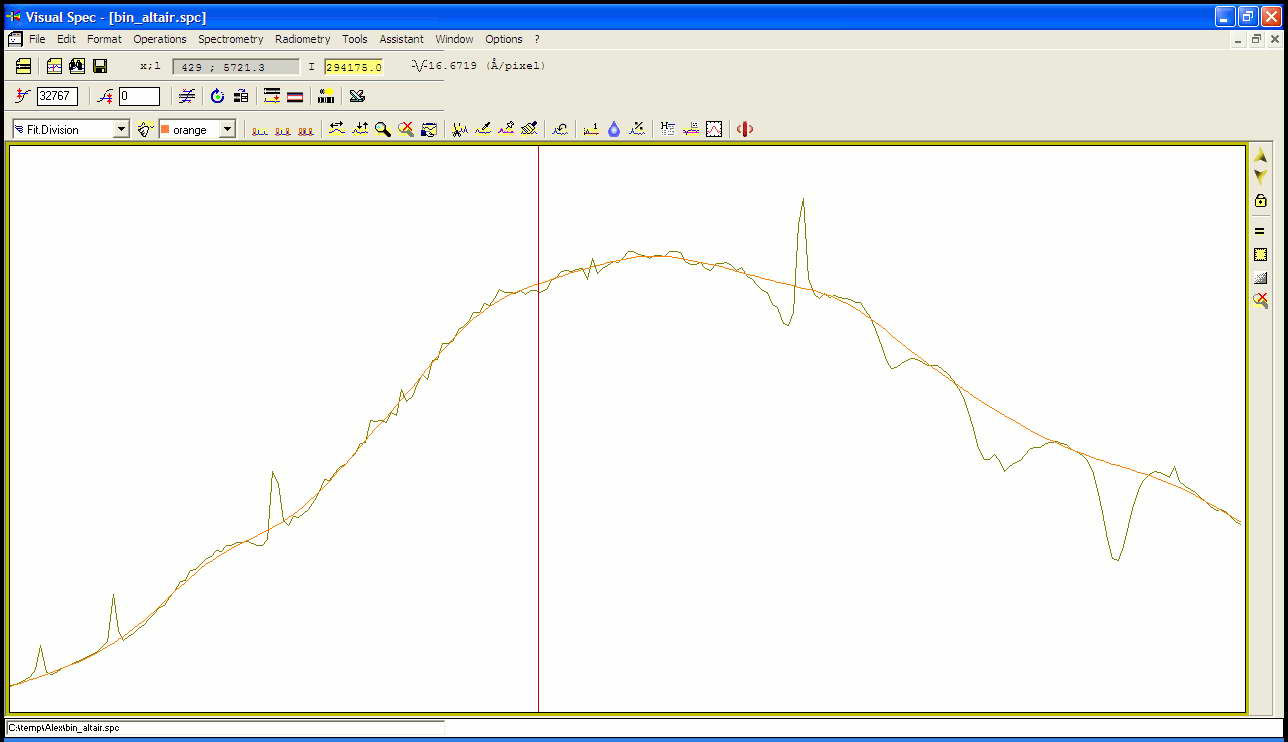
Fig. 5 : profil spectral d’Altair
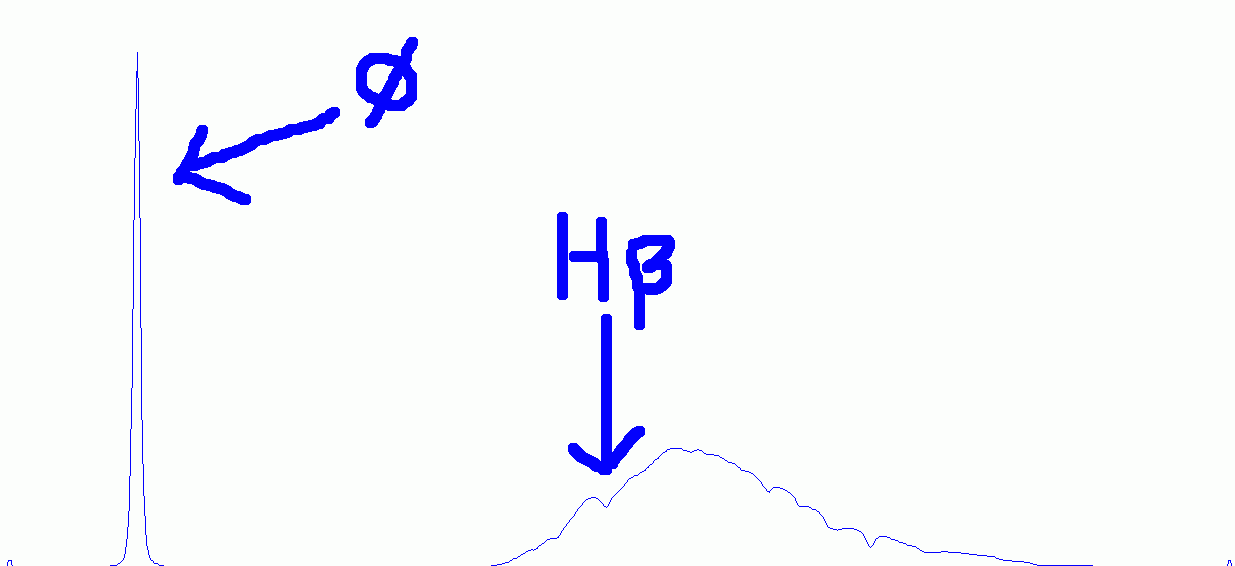
La figure 5 montre le graphe du profil spectral de l’étoile Altair. Il est recommendé de commencer avec une étoile de type spectral A (Vega, Regulus, Altair…) dont le spectre comporte essentiellement les raies d’absorption de l’hydrogène (série de Balmer: Ha / H-alpha, Hb / H-beta, etc…). Le profil montre toutefois d’autres creux dans la courbe; ce sont des bandes d’absorption de l’atmosphère terrestre et des irrégularités dans la courbe de réponse spectral du système (notamment le capteur CCD).
On note aussi le grand pic à gauche qui correspond à l’ordre zéro, c’est-à-dire l’image de l’étoile. Cet ordre zéro est très utile car il correspond aussi à la longueur d’onde théorique de zéro. La dispersion d’un réseau étant linéaire, une seule raie suffit pour calibrer le spectre. La raie Hb est souvent la plus reconnaissable. Sa longueur d’onde est de 4861 Angströms. La calibration à deux raies de VisualSpec se fait alors très facilement avec l’ordre zéro et Hb. Noter la dispersion spectrale obtenue (ici: 16.67A/pixel).
Le spectre obtenu est calibré en longueur d’onde. Il est conseillé alors de fenêtrer et de conserver le domaine spectral entre 4000A et 8000A. En dessous, le signal est trop bruité; au dessus, le deuxième ordre du spectre perturbe trop le signal. Il reste maintenant à corriger le spectre de ces irrégularités liées à la courbe de réponse spectral de l’instrumentation.
Pour cela, on utilise la bibliothèque de spectre standard de VisualSpec. Dans le cas d’Altair, on choisit le standard A7V (un coup d’oeil avec l’outil SIMBAD du CDS / Centre de Données astronomiques de Strasbourg permet de connaître le type spectral à utiliser). Diviser alors le profil spectral d’Altair par le profil standard d’une étoile de type A7V ; le résultat est la courbe de réponse spectrale de l’instrumentation qu’il convient toutefois de lisser pour éliminer les artéfacts locaux :
Fig. 6 : lissage de la courbe de réponse instrumentale
La température du profil de la biliothèque étant de 10000K, nous divisons également la courbe de réponse par la division entre la courbe de Planck de 10000K par celle de température 7750K, la température catalogue d’Altair.
Pour tous les autres spectres pris dans les même conditions instrumentales, la calibration est plus simple et se fait sur une seule raie: l’ordre zéro; il suffit d’indiquer à VisualSpec la dispersion trouvée sur le premier spectre (16.67A/pixel dans notre exemple). Ensuite, diviser le profil spectral par la courbe de réponse instrumentale afin d’obtenir le spectre final.
Résultats
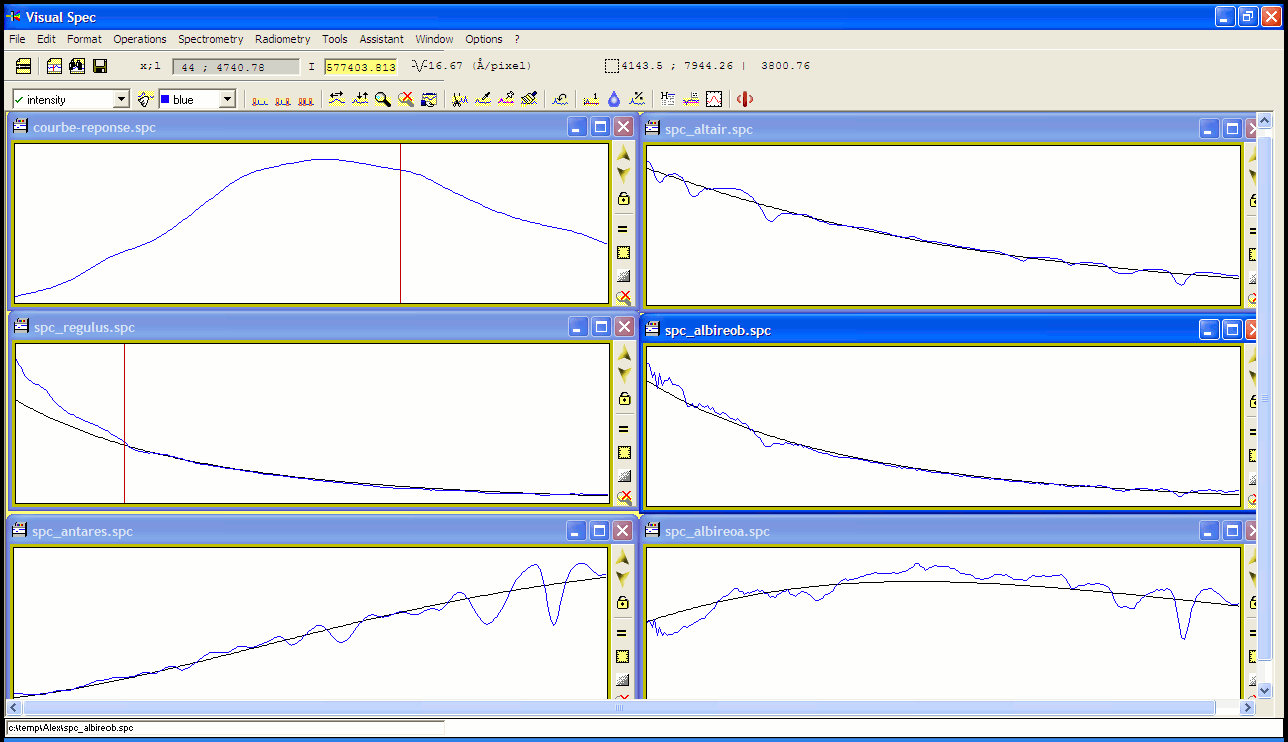
VisualSpec possède, entre autre, une fonction très sympathique qui permet à partir d’un profil spectral de rechercher automatiquement la température correspondant au profil de Planck le plus proche du spectre. La suivante montre le résultat sur plusieurs spectres avec cette fonction « auto-planck » (recherche entre 2000 & 30000K par palier de 100K).
Fig. 7 : spectres de plusieurs étoiles avec la courbe de Planck la plus proche
Les températures mesurées par profil de Planck sont les suivantes:
- Spica (B1III): 18800K [catalogue: 22400K; erreur: 18%]
- Regulus (B7V): 17700K [catalogue: 15400K; erreur: 15%]
- Albireo B (B8Ve): 11800K [catalogue: 12000K; erreur: 2%]
- Deneb (A2Iae) : 9900K [catalogue: 8400K; erreur: 18%]
- Altair (A7V): 7700K [Kaler: 7750K; erreur: 1%]
- Saturne (Soleil: G2V): 5300 [catalogue: 5700K; erreur: 7%]
- Albireo A (K3II+…): 4200K [catalogue: système binaire 4400K/11000K; erreur: ~15%]
- Antares (M1.5Iab-b): 2800K [catalogue: 3500K; erreur: 20%]
Erreurs de la méthode
Nous avons pris comme référence une étoile de 7750K ; les erreurs obtenus croissent logiquement quand on s’éloigne de cette température étalon.
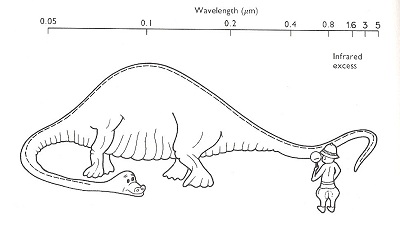
Pour les étoiles chaudes, nous n’observons qu’un bout de la courbe de Planck. L’astronome anglais Norman Walker utilise la comparaison avec l’explorateur qui découvre la queue d’un animal et doit trouver à quel type de dinosaure elle appartenait – l’incertitude est grande :
Fig. 9 : profils de Planck dans le domaine visible
La méthode a également ses limites car le spectre observé d’une étoile n’est pas exactement un profil de Planck:
- La diffusion de la lumière par la matière interstellaire et par notre atmosphère (si les étoiles et l’étoile de références pour la courbe de réponse instrumentale ne sont pas observées à la même masse d’air) rougissent les étoiles et déforme le profil global du spectre
- Les raies d’absorption photosphériques abaissent le profil global; c’est le cas des étoiles de type M par exemple – nous ne voyons pas le continuum mais que les absorptions qui se mélangent !
- Une émission continue dans le domaine visible peut accroître le profil global; c’est le cas des étoiles Be par exemple (comme Albireo B) avec une émission « free-free » qui s’ajoute au continuum et peut même représenter 70% du continuum…
- Enfin, une étoile n’est pas exactement un corps noir de température unique; c’est une approximation que nous faisons dans le cadre de cette méthode.
Conclusions
Il est amusant de mesurer les températures des étoiles depuis son jardin avec une incertitude acceptable au vu des moyens employés. Auguste Comte avait tort: la mesure des températures à distance nous est accessible – c’est la magie de la spectroscopie et des lois astrophysiques développées depuis maintenant deux siècles.
Des méthodes plus modernes existent toutefois pour mesurer des températures plus précises, notamment avec un spectrographe de beaucoup plus haute résolution comme le Lhires III. La première repose sur les propriété d’ionisation des atomes en fonction de la température (équation de Saha); la mesure de rapports d’intensité de raies d’absorption est d’ailleurs à la base de la classification spectrale et de l’ordre étrange de l’alphabet spectral: OBAFGKM. Une autre méthode plus utilisée de nos jours par les astronomes professionnels consiste à modéliser le spectre à partir de modèles théoriques dont la température effective est un des paramètres clefs.
La mesure a l’avantage de donner des résultats rapidement – de surcroît avec de faibles moyens dans le cas du Star Analyser. Je vous encourage à tenter l’expérience vous-même: vous « sentirez » la chaleur des étoiles vous envahir !
Références :
Fichiers images pour refaire les calculs : https://www.shelyak-instruments.com/Web/star_Analyser/Tutorial%20Data%20-%20Star%20Analyser%20(alex).zip
Acker Agnès, « Astronomie Astrophysique » ; Dunod, 2005.
CDS / Centre de Données astronomique de Strasbourg; l’outil SIMBAD : http://simbad.u-strasbg.fr/simbad/sim-fid
Cooper W.A., Walker E.N., « Getting the measure of the Stars »; édition Adam Hilger, 1980.
Gallica: la bibliothèque numérique de la Bibliothèque Nationale de France (chercher entre autres les ouvrages de Auguste Comte ou du père Secchi…) : http://gallica.bnf.fr/
Gouguenheim L., « méthode de l’astrophysique »; Hachette, 1981.
Hearnshaw J.B., « the analysis of starlight » ; Cambridge University Press, 1986.
IRIS : http://astrosurf.com/buil/iris/iris.htm
Kaler James B., « Stars »; Scientific American Library, 1998.
Kaler James B., « Stars and their spectra »; Cambridge University Press, 1997.
VisualSpec : http://astrosurf.com/vdesnoux/